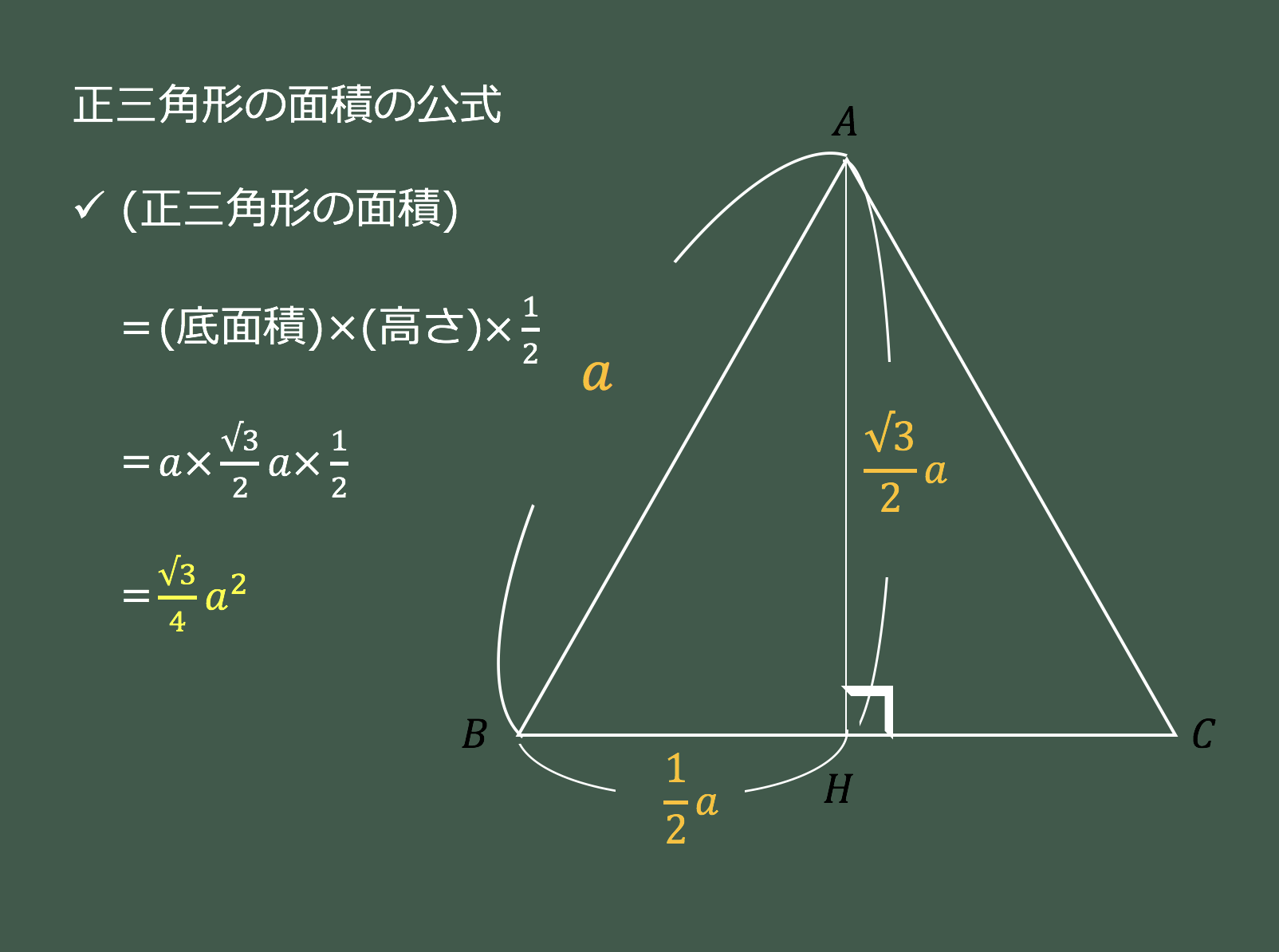
正三角形を作図するための考え方 正三角形とは、すべての辺の長さが等しい三角形のことですね。 ということで、 円の中に3辺がすべて等しくなるような三角形を作図したい です。 どのように同じ長さの辺をとるかというと 正三角形と直角三角形 正三角形はすべての角度が60°。 正三角形を半分にすると「30°、60°、90°の直角三角形」になり、 一番長い辺が一番短い辺の2倍の長さになる 。 三角形の面積の公式―底辺×高さ÷2 三角形の面積の公式は 「底辺×高さ÷2」 です。(半正矢関数の公式) また、各三角形の面積を足し込む際の正負は、外積の正負から判定する。 → cosφ0×cos𝜆0 cosφ0×sin𝜆0 sinφ0 cosφ𝑖×cos𝜆𝑖 cosφ𝑖×sin𝜆𝑖 sinφ𝑖 cosφ𝑖1×cos𝜆𝑖1 cosφ𝑖1×sin𝜆𝑖1 sinφ𝑖1 >0ならば1 そうでなければ1 以下
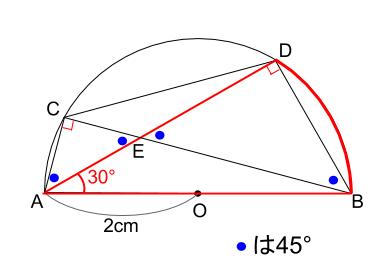
円の総合問題 その4 30 の利用 中学数学の無料オンライン学習サイトchu Su
正三角形と半円 面積
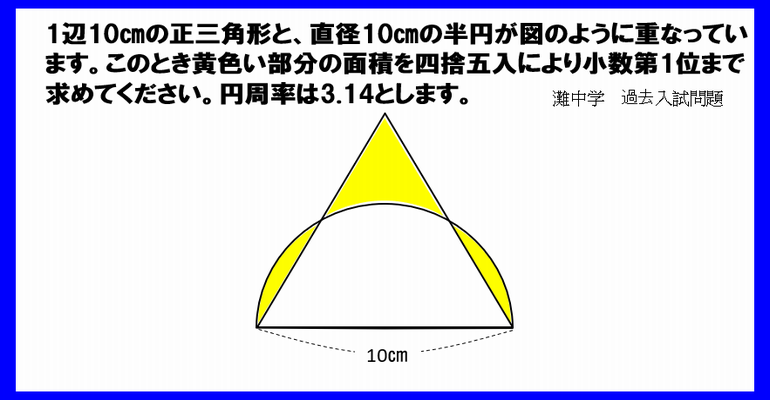
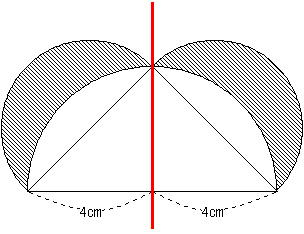
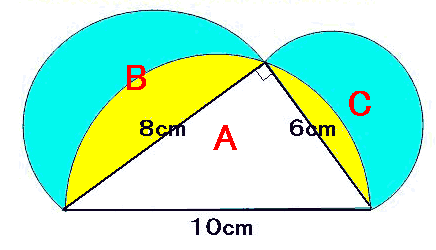
正三角形と半円 面積-1 おうぎ形から直角二等辺三角形を引く 1 =16×π−32 =5024−32 =14(㎠) 弓形の面積=おうぎ形−直角二等辺三角形 2 赤いおうぎ形−斜線の三角形 1 =456(㎠) 3 斜線の弓形を求めて2倍する 1 =114(㎠)弓形1個分(☆) 4 半円−直角二等辺三角形 正三角形と半円(灘中学 受験算数問題より) ただし、等積である根拠が必要。 「なんとなく・・・」は息子の得意分野です。 1辺10cmの正三角形と、直径10cmの半円が図のように重なっています。 このとき黄色の部分の 面積を小数第1位まで求めなさい



1
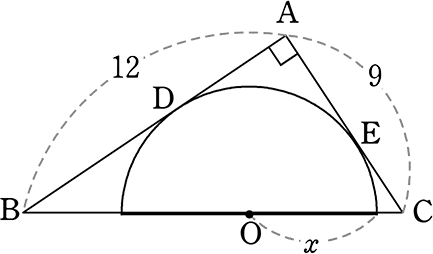
正三角形の面積二等分線(18都立青山) 都立高校入試では、作図問題が必ず出題されています。 苦手とする人も結構いるようですが、幾何の原理をしっかり理解できていれば何のことはないはずです。 中でも、"面積二等分線"は作図の定番なので 本記事では、周長の等しい正多角形の面積の極限について説明します。 正多角形の面積 先ずは、一辺の長さがaである正n角形*1の面積を考えます。 図1 正多角形の一部を構成する二等辺三角形 正n角形は、その中心から各頂点に引いた線分によってn個の二等辺三角形に分割されたます。 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げています。 図形ドリル 半円の中に直角三角形と2つの円がぴったり入っています。AB=12 cm,AC=16 cm,BC= cmのとき,2つの円の面積比は何対何ですか
図を見てみよう。例として、正六角形と、正八角形が挙げられているね。このように対角線を結んでみると、 正六角形 なら 6個 、 正八角形 なら 8個 の 三角形 に 等分 できるよ。 だから、 正n角形 の面積を求めるときは、等分した 三角形の面積 を求めて、 n倍 してやればいいんだ。正三角形の面積 三角形の面積(底辺と高さから) 三角形の面積(2辺と夾角から) 三角形の面積(3辺からヘロンの公式) 三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから) 三角形の面積を求めるためには 一旦、平行四辺形の面積を求め それを半分にしている。 だから、2で割る必要があるんですね! 忘れないように覚えておきましょう(^^) 三角形の面積を求める問題 それでは、三角形の面積公式を使って問題を解いていき
面積の計算 ・ 正三角形の面積 ・ 三角形の面積 (底辺と高さ) ・ 三角形の面積 (2辺と間の角度) ・ 三角形の面積 (1辺と両端の角度) ・ 三角形の面積 (3辺の長さ) ・ 正方形の面積 ・ 長方形の面積 ・ 台形の面積〔特別角の三角形 問 題編〕 類題 4 右の図は,線分 OA を半径とする円O と,線分OA の 垂直二等分線をかいたものです。OA=4cm のとき,図 のかげ( )をつけた部分の面積を求めなさい。ただし, 円周率をπとします。 類題 5 図は,半径 三角関数の2倍角の公式・半角の公式の証明と応用 スポンサーリンク 高校数学Ⅱ 三角関数 検索用コード 証明は容易で,\ \bm {加法定理において\ \beta\ →\ \alpha\ }とするだけである \bm {利用機会が極めて多い}ので,\ 毎回加法定理から導くというのは



ヒポクラテスの三日月 面積は 中学入試 出題多数 パズル おもしろ算数問題



中学受験 算数
正五角形の面積(東海 04) 正三角形と正六角形 平面図形の面積 (三田学園 1998 改題) 正六角形の部分の面積(sapix補充算数プリントより) 半円とおうぎ形の面積(sapix算数補充プリント) 正三角形と半円(灘中学 受験算数問題より) 直径6の半円と、1辺が6の正三角形。 半円の直径と三角形の底辺が共通。 右下の三角形も、左下の三角形も、 1辺が3の正三角形になりそうですが、、、。 そのことの証明と、あとはどの図形とどの図形を組み合わるか、 の2点がポイントになりそうです。採点する やり直す 解説 3 半径 10 ,中心角が90°の扇形の面積 円の面積の4分の1だから,10 2π ÷4=25 π π 採点する やり直す 解説 4 下の図の灰色で示した図形の面積 扇形の面積は円の4分の1で25 π ,これから三角形の面積 10×10÷2=50 を引く



小学6年生の娘の宿題 図の灰色部分の面積を求めよ という問題です Yahoo 知恵袋




半円に内接する2つの正方形の面積の和 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog
三角形abcは正三角形の半分なので、 ac:ab=2:1。 三角形abcと三角形gdcと三角形fec は相似。 feを②とすると、fc=④。 三角形gefは二等辺三角形なので、 gf=②。よってgd=ag=③。 三角形abcと三角形fecの相似比は9:4、面積の比は81:16。A=面積 鋭角三角形 鈍角三角形 台 形 不平行四辺形 なお点線にて示すごとく二つの三角形となし、各々の面積を計算し、 その和をもって不平行四辺形の面積を算出してもよい。 a=面積 正六角形 正八角形 正多角形 円 a= 正三角形の面積の求め方を3ステップで伝授しよう。 さっきの正三角形ABCの面積を求めていくよ。 Step1 頂角から二等分線をおろす 頂角の二等分線を底辺にひいてみよう。 頂角が半分になる線をすーーーっと底辺にひけばいいのさ。 AからBCにむかって二
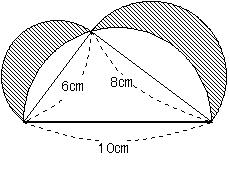



ちょっとだけ反則っぽい 暗記 を活用しよう 前田昌宏の中学受験が楽しくなる算数塾




第23回 円の転がり 算数ドクター
正三角形の辺を入力 辺 a = 1 面積 S = 0433 正三角形の辺を入力 辺 a = 23 面積 S = 2291 このように正三角形の面積を計算してみました。 その他のサンプルプログラムも合わせてご覧ください。 C言語のサンプルプログラム集入試解説 6年生 男子校 5年生 正方形 正三角形 東京 兵庫 灘 算数オリンピック 共学校 面積比 円 図形NOTE logix出版 角度 1日目 直角三角形 4年生 女子校 相似 立方体 長方形 おうぎ形 30度 正六角形 16年 17年 19年 トライアル 18年 年 ファイナル 二等辺三角形 直角二等辺三角形 21年 立体の三角形ABCの面積が85c㎡のとき、三角形ADEの面積を求めなさい。ただし、辺BCは5等分されています。 → 解答 問題5 次の直角二等辺三角形の面積を求めなさい。 → 解答 問題6 面積が0c㎡の2つの正方形が、図のように重なっています。




発展 直角三角形の面積とsin28 なかけんの数学ノート
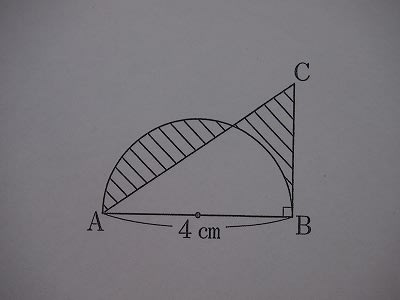



15年2月のブログ記事一覧 マッキーのつれづれ日記



3




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく



算数 三日月形 半円 の面積の応用問題の答 なるほどの素




中学受験算数 等積変形の利用 ヒポクラテスの月




斜線部の面積を求める 1 Youtube




正三角形 の作図方法 コンパス 定規 数学fun
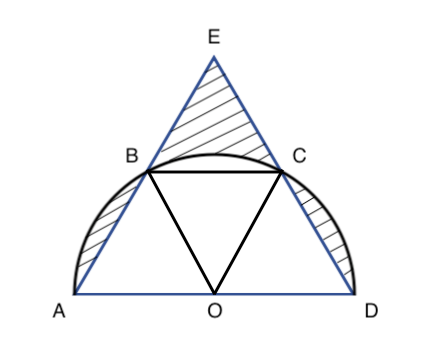



斜線部分の面積を求める問題 よくあるパターン 苦手な数学を簡単に




正四面体 空間図形に含まれる三角形の面積を求める問題 数学i By ふぇるまー マナペディア



中学の数学の図形問題についてお聞きします 1辺の長さが10cmの正三角形と Yahoo 知恵袋



しょうちゃん 公式ブログ 算数の問題を解いてみる その15 図形 円の面積 Powered By Line




中3数学 正三角形に半円が内接 接線の長さ 三平方の定理の応用 Youtube




円の総合問題 その4 30 の利用 中学数学の無料オンライン学習サイトchu Su



灘 開成 麻布 超難関校に挑戦 円周率 の引っかけ問題 富裕層向け資産防衛メディア 幻冬舎ゴールドオンライン



教えて下さい 下記の図はアイを直径とする半円と直角三角形アイウ Yahoo 知恵袋




直感的に求めよう 直角三角形の面積の求め方 パパが教える算数教室




高校入試数学 中学入試でも頻出の直角三角形と半円の問題 Youtube
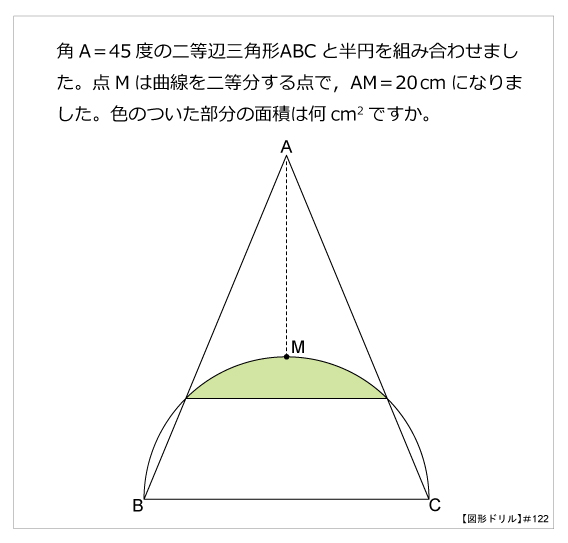



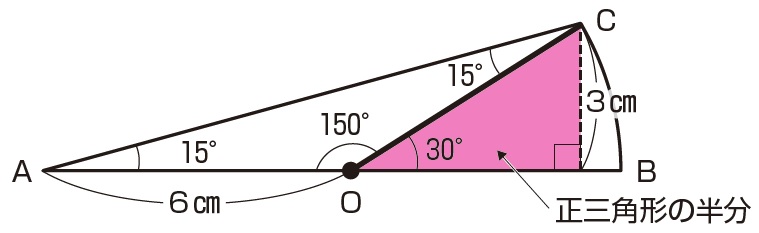
図形ドリル 第122問 半円と二等辺三角形 算数星人のweb問題集 中学受験算数の問題に挑戦
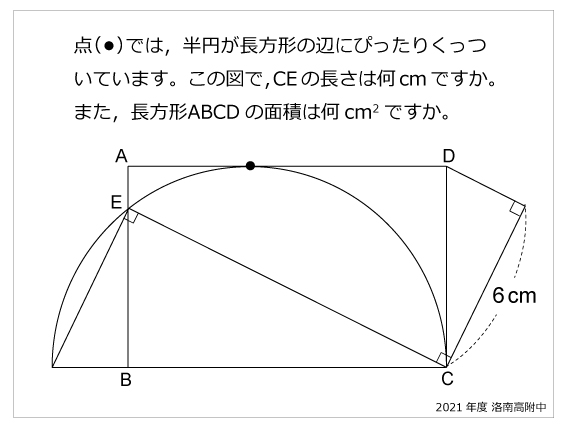



半円 算数星人のweb問題集 中学受験算数の問題に挑戦
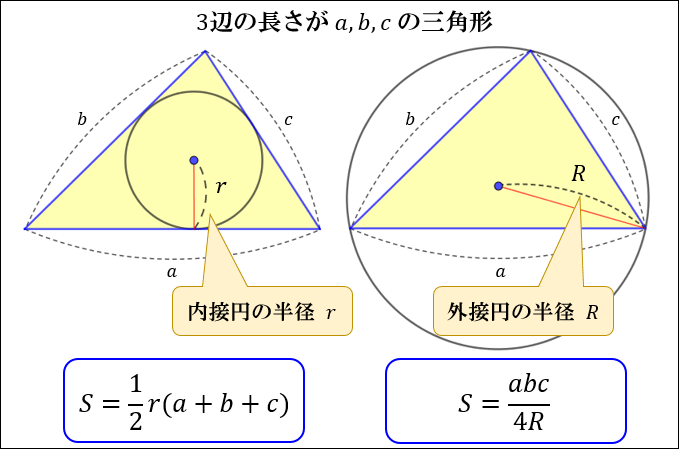



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
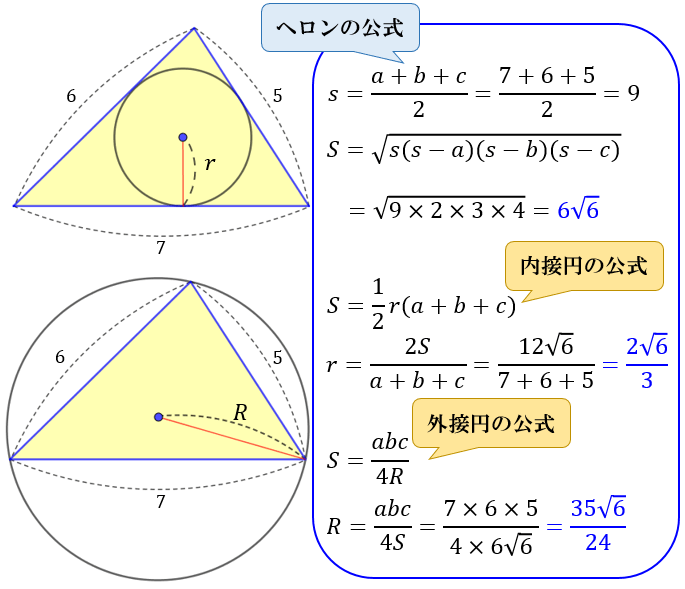



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




この問題の解き方を教えてください Clear



三角形の面積と公式 面積計算機



第14問の解答




中心角1 の弓形に内接する正三角形の面積 香料ゐっすゐの夢



中学受験 ヒポクラテスの定理 学ぶ 楽しむ 世界を泳ぐ ができる数理の世界




半円と直角三角形 算数の広場



算数問題 全2問 中学入試で出題された難問 子供から大人まで動画で脳トレ 楽天ブログ



1辺の立方体に収まる正三角形の最大面積はいくらですか Quora



図のように直角三角形に半円が内接しているとき この半円の直径を Yahoo 知恵袋



正三角形と半円 灘中学 受験算数問題より どう解く 中学受験算数



半円と正三角形を組み合わせたものです 影の部分の面積求めなさい 答え42 Yahoo 知恵袋



半円と正三角形を組み合わせたものです 影の部分の面積求めなさい 答え42 Yahoo 知恵袋
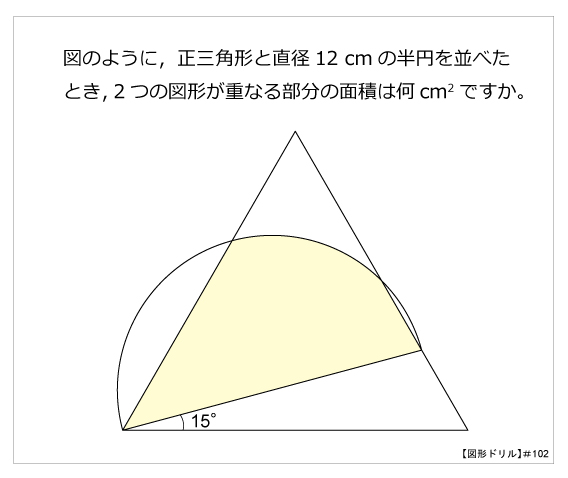



図形ドリル 第102問 正三角形との共通部分 算数星人のweb問題集 中学受験算数の問題に挑戦
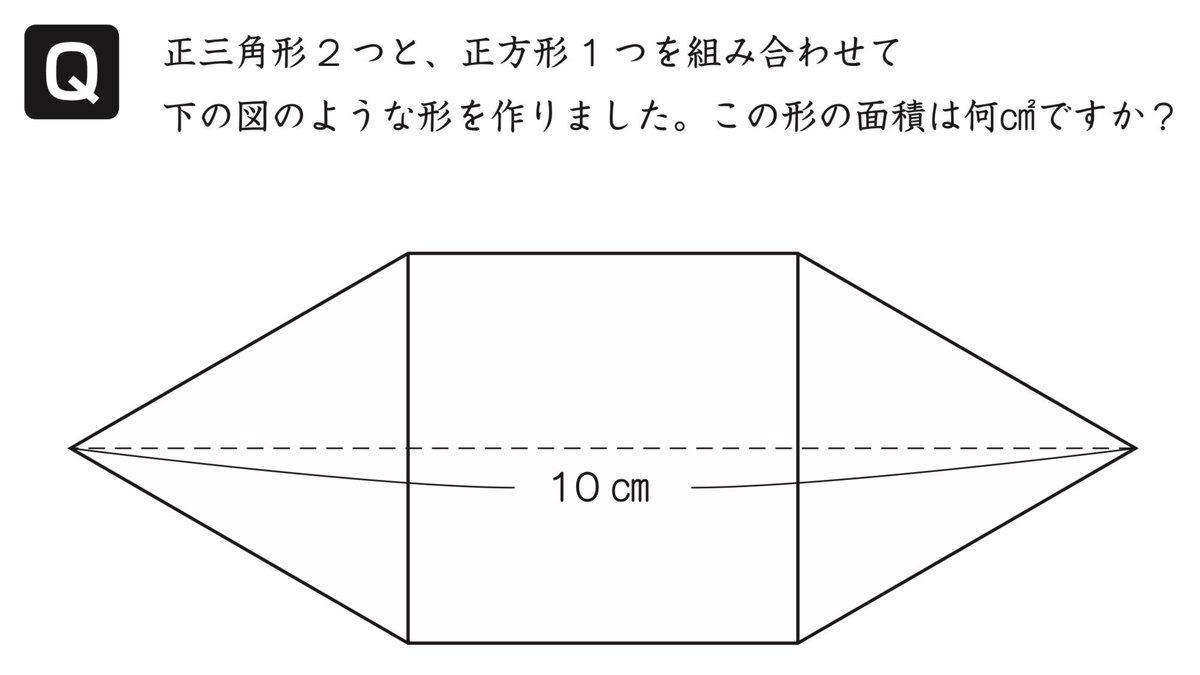



小学校で習う知識だけで解けます ルートも使いません 東大生が小3のときに作った算数の問題 Togetter



積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典
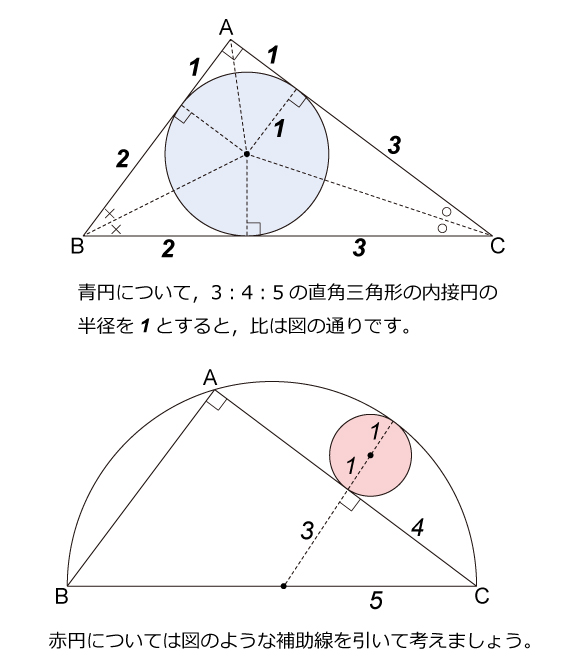



図形ドリル 第87問 半円と三角形と内接円 算数星人のweb問題集 中学受験算数の問題に挑戦



図形の和と差



正三角形と半円 灘中学 受験算数問題より どう解く 中学受験算数




中学受験算数 等積変形の利用 ヒポクラテスの月



気まぐれリクエスト解説 平面図形 2つの半円を30度重ね合わせた図形の面積 気まぐれ解説カフェ 仮



Math 円の問題を解くときに使う3つの技 全体 白 分配法則 移動 働きアリ




算数星人 New 図形ドリル 第299問 正三角形と面積の差 T Co Lvgyfp4tfq 分からないときはヒントを見てね




民報チャレンジ18 数学15 図形の面積 N Kaneta Blog




N013 Descubre Como Resolverlo En Qanda
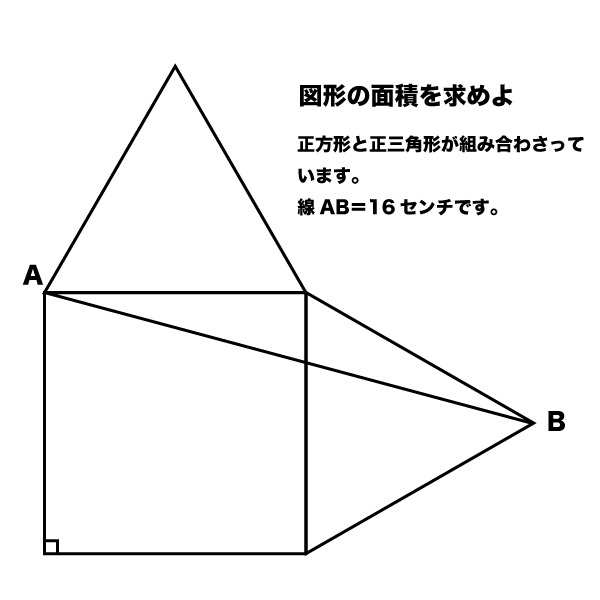



正方形と正三角形が組み合わさった図形の面積計算 受験算数入門




答193 正三角形と半円 ヤドカリの 気ままな数学




最高 50 正三角形 面積 求め方
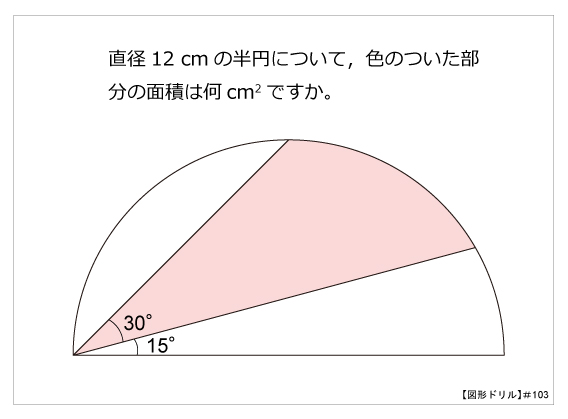



図形ドリル 第103問 半円の中の図形 算数星人のweb問題集 中学受験算数の問題に挑戦




中3数学 正三角形に半円が内接 接線の長さ 三平方の定理の応用 Youtube



斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める



円は大地主 理科好き子供の広場



ちょっとだけ反則っぽい 暗記 を活用しよう 前田昌宏の中学受験が楽しくなる算数塾




同じ広さはどこ 半円と正三角形 Geogebra



腕試し問題 幾何の問題 江戸の数学




R2 7月の算額から 図のように長方形の土地を3本の斜線で仕切る 甲の面積が90坪 乙が80坪 丙が1坪ならば丁の面積は何坪か 答 丁は 21 坪 解答例はここです Pdf R2 4 5月の算額から 図のように



簡単公式 正三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




直角二等辺三角形の面積を求める公式は 覚えずに自分でつくろう



Http Www Suguru Jp Pdf Yokude Yokude Php




算数図形編 面積 線分の長さ 対称な図形を追加してみよう 中学受験 高校受験パスナビ



3




中学受験の円に関する問題 角度 長さ 面積の基本問題まとめ 算数数学苦手克服 家庭教師のマスコンサルティング



1




中学受験算数 平面図形編 Flashcards Quizlet



投稿1080




最高 50 正三角形 面積 求め方
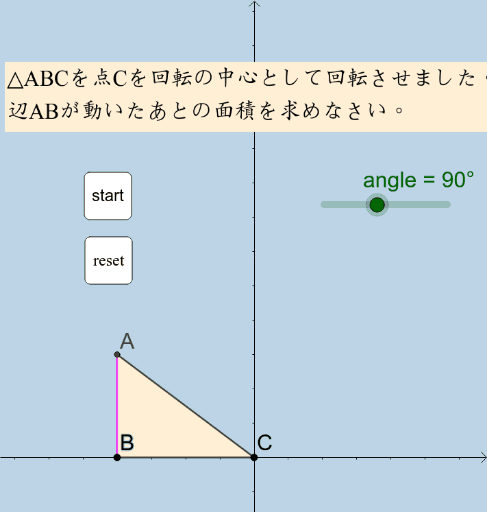



同じ広さはどこ 半円と正三角形 Geogebra




記事一覧 数学クイズ なん度 Math Quiz Find Angles




直角三角形 Wikipedia




教えてください 6cmです Clear




2 Lihat Cara Penyelesaian Di Qanda




平面図形 どう解く 中学受験算数
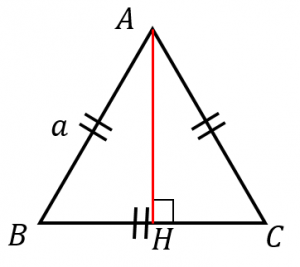



正三角形の面積の求め方 小学生用 高校生用 具体例で学ぶ数学



数学の美しさ
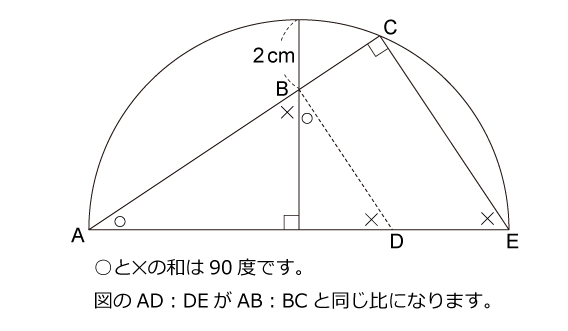



図形ドリル 第224問 半円と直角三角形 算数星人のweb問題集 中学受験算数の問題に挑戦



円と三角形



Math Battle 0226 半円の接線の長さ



Math 90 30 60 の直角三角形 辺の長さで成り立つこと 働きアリ



算数 三日月形 半円 の面積の応用問題の答 なるほどの素



正方形と正三角形が組み合わさった図形の面積計算 受験算数入門



中学数学 円周角 中心角



解答 きのっぴぃの旅行記




おうぎ形の面積に関する標準問題3選




ヒポクラテスの定理 Wikipedia



問題93おうぎ形の面積



単位円上にある異なる3点がつくる三角形の面積の最大値をどう求めますか Quora




正三角形及びその内接円に接する円 半円 香料ゐっすゐの夢



Www Ksen Ac Jp Files Zukei Pdf



3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ



Math Battle 0227 広世正憲 無限段重ねの半円の面積総和




中1の問題です 一辺4cmの正三角形斜線部の面積は 中1なのでルート 数学 教えて Goo



正三角形の面積の求め方 小学生用 高校生用 具体例で学ぶ数学



一辺が1の正三角形の中に半円が無限に積み重なっています これらの半円の面積総和は正三角形の面積のだいたい何 になるでしょうか Quora
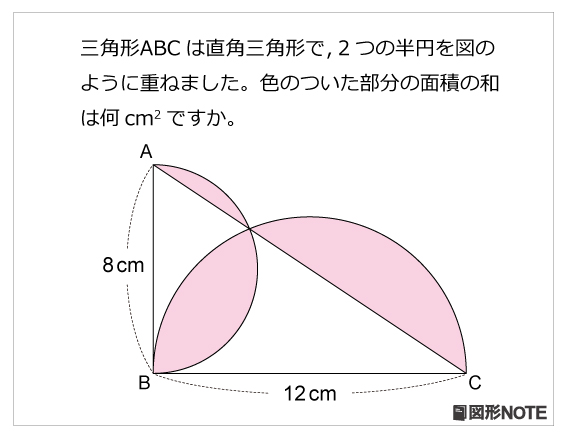



半円 算数星人のweb問題集 中学受験算数の問題に挑戦



1




正三角形及びその内接円に接する円 半円 香料ゐっすゐの夢



無料 中1数学 発展問題 解答プリント 空間図形1 展開図 多面体



0 件のコメント:
コメントを投稿